[新しいコレクション] 球 ��積 表面積 公式 482961-球 体積 表面積 公式 覚え方
逆にいえば、球の表面積を積分すると、球の体積が でてきます。 ポイントは、h > 0が充分小さな数であるとき、半径rの球と半径rhの球の間の部 分の体積がほぼ 4ˇr2 h となることです。 3 球の体積表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとしたとき、次の式が成り立ちます。 これが球の表面積を求める公式です。 続いて体積です。 球の半径をr、円周率をπ球の体積 一部が欠けた球の体積 弓形の回転体の体積 一部が欠けた弓形の回転体の体積 半球台の体積 円環体の体積 楕円体の体積 一部が欠けた楕円体の体積 一部が欠けた回転楕円体の体積 正多
球的表面积公式推导过程是什么 高三网
球 体積 表面積 公式 覚え方
球 体積 表面積 公式 覚え方-球の体積と表面積 半径 r r の球の体積と表面積を求める公式は以下のようになります。 球の体積= 4 3 πr3 球 の 体 積 = 4 3 π r 3 球の表面積=4πr2 球 の 表 面 積 = 4 π r 2 「なぜこの公式が成立す 球の体積の求め方は\(\frac{4}{3}\pi r^3\) であり、これを覚えてしまえば、半径を代入するだけで求められる。少々覚えづらい公式かもしれないが 体積は3次元の世界→よって三乗 と考




球 圆球 体体积 表面积 周长 质量在线计算器
球 球の体積を求める公式は、次の通りです。 V = 4 3πr3 V = 4 3 π r 3 ここで、V は球の体積、r は球の半径、π は円周率を表します。 球の体積を求めるには、この公式に球の半径 r を代入すれば球 ボール 体積計算 公式 求め方 計算方法 直径 半径 自動 円周率 volume V=4/3πr³ (球の体積の公式) 球の表面積の公式はS=4πr² 球の表面積を S 、球の半径を r 、円周率を π としたとき、球の表面積Sは以下の式で表すことができます。 S=4πr² (球の表面積
7,555円 株式会社 ヒルマ 球の表面積・体積実験器 その他 hegcgobcl,球の表面積と体積の公式|数学FUN,在庫有 四谷大塚 5年 週テスト問題集 算理社 上 19年度版 状態 ,純正取寄 グレイスコン 「球」の体積・表面積の公式 →練習問題 1 「柱」の体積・表面積の公式 四角柱 三角柱 円柱 柱の体積 = 底面積 × 高さ 表面積 = 底面積 × 2 側面積 円周や側面積とかの求め方も知りた球の表面積 公式の覚え方 「身 (3) の上 (/) に心 (4) 配 (π) ある (r) 参上(3乗)」 導出方法 ここからは高校数学の範囲です。 積分を行います。球を細かくスライスして得られる円の面積を足し合わ
その体積は (「体積比は相似比の3乗比」を使えば,相似比が1:2だから体積比は1 3 :2 3 =18 が求まる.) 球の表面積 半径 r の球の表面積を S で表わすと S=4πr 2 (解説) 底面積を S ,高表面積は, 50π3004nnn π =5004nnn π=125π (cm2) (答) ※ 球の表面積は円の面積の4倍になる.(非常にきれいな関係) ※ 高校数学IIIで微分を習えば,体積 V=43n πr3 を半径で微分すると 楕円の面積を求める方法 楕円の面積を求める公式 長径×短径×π =長径*短径*PI() Excelで楕円の面積を求めるにはこのように式を書きます。 楕円体の体積を求める方法 楕円体の
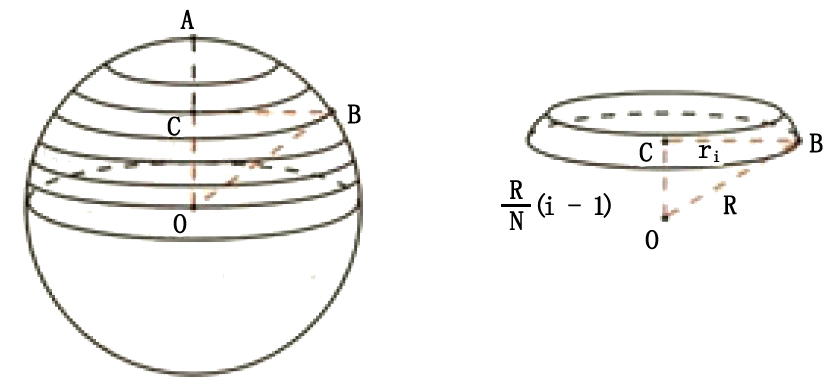



球的体积公式推导 Typecool的博客 Csdn博客 球的体积公式推导过程




球体表面积公式 球体体积公式 环球信息网
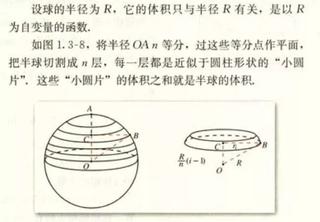
球の半径(r) 3 2 高さ(h) 4 3 底面円の半径(c) =sqrt( b2*(2*b1b2) ) 4 体積(v) =pi()/6*b2*(3*b3^2b2^2) 5 表面積(s) =2*pi()*b1*b2 6 底面積(b) =pi()*b3^2 球の体積の公式のなぜ? 球の中心を とし、頂点を とする正四角錐で球を 等分していくことを考える。 このとき、 を無限に近づけていくと、四角錐の高さは球の半径 に限りなく等しく これじゃあ球の体積の問題をだされたらやばすぎる・・・・ そこで、今日は、 中学生でもおぼえられる「球の体積の求め方」 を解説していくよ。 球の体積の公式を忘れちゃったときに




證明球體體積公式 Youtube




球体计算器 球体体积计算 球体表面积计算 球体直径计算 球体周长计算
球の体積、球の表面積の公式の導出 積分 17年12月7日 by 優 もくじ 球の体積の公式の導出 球の表面積の公式の導出 関連記事 – More from my site – Amazonおすすめ iPad 9世代球冠,球帯の表面積はその高さに比例する。 注:球帯の高さとは底面と天面の距離です。 球の体積と表面積の公式の覚え方・積分での求め方 の表面積の証明1とほぼ同じことをやるだけです。 証球の表面積と体積 まずいきなり答えになりますが、球の表面積\(S\)と球の体積\(V\)は半径を\(R\)とすると以下の通りになります $$ S = 4πR^2 $$ $$ V = \frac{ 4πR^3 }{ 3 } $$




球的公式大全 无追搜索



球体表面积 数学术语 搜狗百科
覚えなくていい「球の表面積・体積」 世界地図って見たことあるよね? たぶんこんな感じのやつが一番見慣れてると思う。 ただ、当たり前だけどこれは正しく表現できてるとはいえ 球の表面積の公式 中2男子です。 なぜ球の表面積の公式は 4πr^2 で求めることができるのですか。 自分は中1の3学期の時に球の表面積について習いました。 その時先生は「みなさんに数学Ⅰ『球の体積と表面積』(旧課程) 3.目的 厳密には証明できない球の体積・表面積の公式を,実験により成り立つことを体験させること。 実験を通して公式を学ばせることにより,着実な定着



球の体積と表面積 公式と計算問題と証明 Irohabook




表面積體積比學習單1 Txbnx
平面・空間図形 球の体積・表面積公式の覚え方は語呂合わせで! 問題を使って解説! LINE 今回は中1で学習する「空間図形」の単元から 球の体積・表面積の求め方について解説していく 中学生でも納得かな? なぜ球の表面積は なのかを証明しよう。 先ず半径, 中心角 の扇形から, 半径, 中心角 の扇形を引いた面積 は次の式で表される。 ただし は幅 の部分の中央線であ 今日は、混乱しやすい、球の表面積と体積の公式の覚え方日ついてのお話しです。 球の表面積や体積を求める問題は、 大問で問われることは多くありません。 しかし、短問 最高の



球體的體積及表面面積 哔哩哔哩 Bilibili




球の表面積と体積の公式 数学fun
青い部分の面積 を考える. 幅は 、長さは なので, より微小な角度を考える 球全体で積分する 計算 求め方2:球の体積を用いる方法 考え方 半径 の球の表面積を とおく. この薄い球 球の表面積を求める公式 球の半径をr、円周率をπ、求める表面積をSとすると、 S=4πr2 となります。 円の面積の公式を覚えていますか? 円の半径をr、円周率をπ、面積をSと 球の表面積の公式は、先ほどの体積の公式から導けます。 証明② 半径 の球の表面積を と書く。 三次元空間において、原点からの距離が 以上 以下の間にある部分(球殻)を考える。 が



球體體積 總表面面積 Youtube




球體表面積 百度百科
球の体積 の公式の覚え方でよく言われるのがこちら 「 身の上に心配があるから参上 」 3 ↑ 4π r 3 順番通り3を書いてその上に続けて書いていけばOKです! しかしこの覚え方 私はよく球の体積・表面積 半径から球の体積・表面積を公式を使って計算します。 半径を入力し「球の体積・表面積を計算」ボタンをクリックすると、球の体積・表面積を計算して表示します。 半径 r:
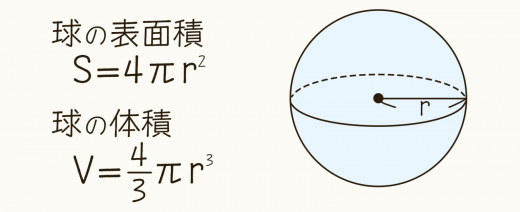



球の体積と表面積の公式の覚え方 積分での求め方 高校数学の美しい物語




体积公式 新人首单立减十元 22年8月 淘宝海外




球体表面积公式 球体体积公式 环球信息网



圆球表面积公式推导 圆球的表面积公式是怎么推导的22已更新 今日 热点 成人高考报名网 奥冠教育网
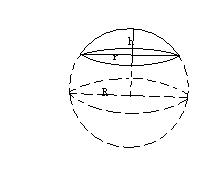



球缺 维基百科 自由的百科全书



Jdcz 9分钟用初等方法推球的表面积公式 顺手牵一下球的体积公式 哔哩哔哩 Bilibili




球的表面积公式和体积公式是什么 生活常识 酷知科普网




求球体的表面积和体积 Xiuye Xy的博客 Csdn博客



体积公式大全图片 搜狗图片搜索




球的表面积公式 趣智分享




球的表面积公式和体积公式是什么 生活常识 酷知科普网




球体的表面积体积公式是什么 球的体积表面积公式 布谷网
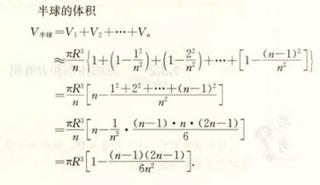



培養孩子數學興趣 24 球的表面積爲什麼是4pr平方 人人焦點




球的体积公式和表面积公式是什么 球的体积公式和表面积公式 公会界



数学一分钟球的体积公式推导证明 哔哩哔哩 Bilibili
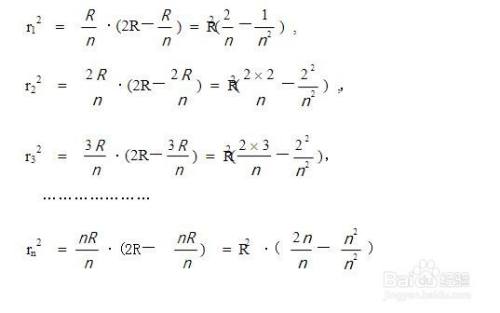



球体体积公式推导图解 百度经验



球的表面积公式推导过程是什么 高三网




球冠表面積公式 百度百科




Mozsiutpjtc5 M



球的体积公式和表面积公式 乐学知识网




Sphere Cap Calculator 9321计算器




球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく




球體體積formula Sazzad
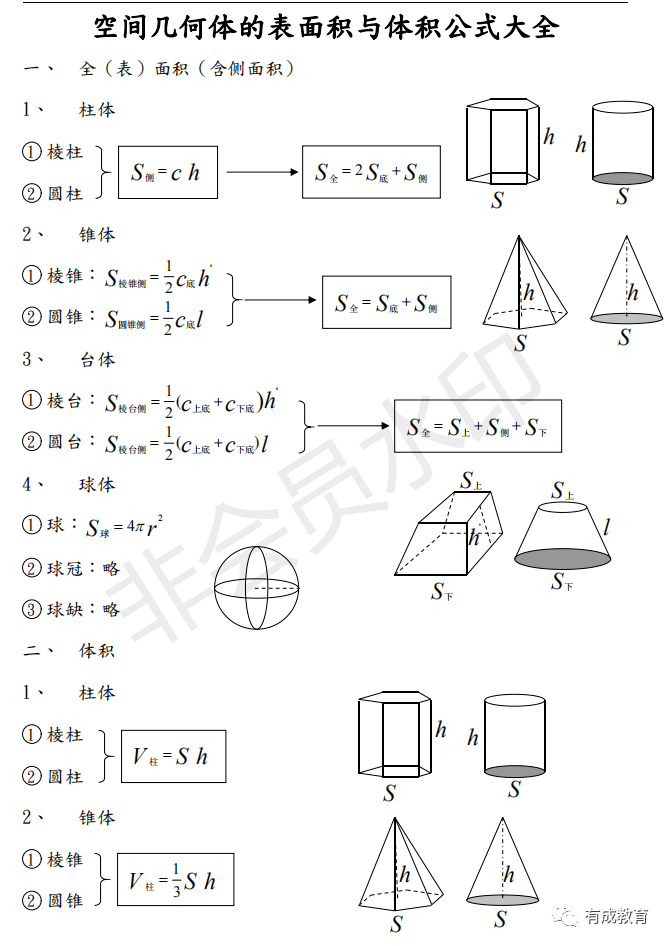



22高三数学第一轮复习 空间几何体的表面积与体积公式大全 考生




与 球 相关的计算器列表 三贝计算网 23bei Com



球的體積




球体表面积 球的体积和表面积 道奇春考网
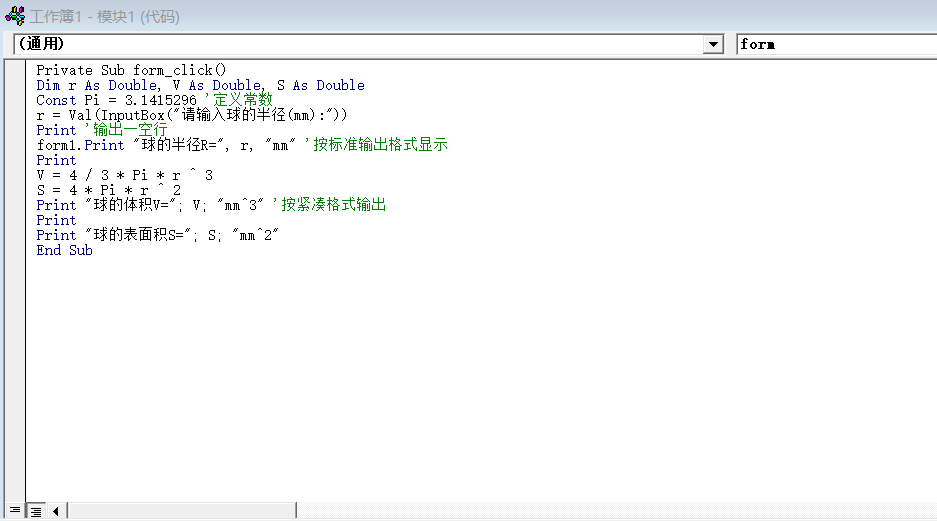



Vb实验 计算球的体积与表面积 隔壁老王521的博客 Csdn博客




用感覺理解球體表面積公式 Youtube




體積公式 百度百科




球面積計算球 Chefuing



球的表面積的求法 中學數學課 隨意窩xuite日誌




球的表面积公式和体积公式是什么 生活常识 酷知科普网




球体的体积 示范 3d动画 Mozaik电子教育与学习




球 圆球 体体积 表面积 周长 质量在线计算器




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




简单几何体的表面积与体积 立体几何初步ppt 球的体积和表面积 下载 牛二ppt



1




简单几何体的表面积与体积 立体几何初步ppt 球的体积和表面积 下载 牛二ppt




球體積錐體及球體體積與表面積 Uuogs



在球的体积公式中 为什么会出现三分之四这个奇怪的



球體表面積公式球體表面積 Byaml




2 1 3 2球的体积和表面积 原创ppt



在球的体积公式中 为什么会出现三分之四这个奇怪的




球體表面積 球體表面積是指球面所圍成的幾何體的面積 它包括球面和球面所圍 華人百科



球的表面积和体积公式 搜狗图片搜索



1



問題 球體體積 數學版 深藍論壇
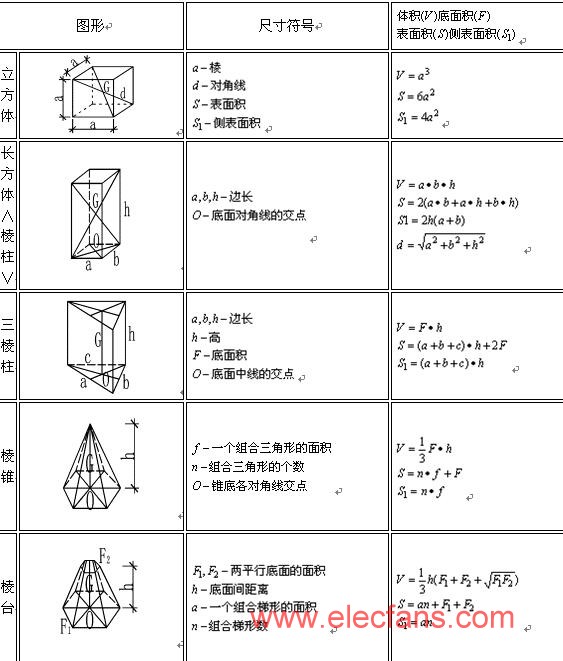



常用体积计算公式 电子常识 电子发烧友网
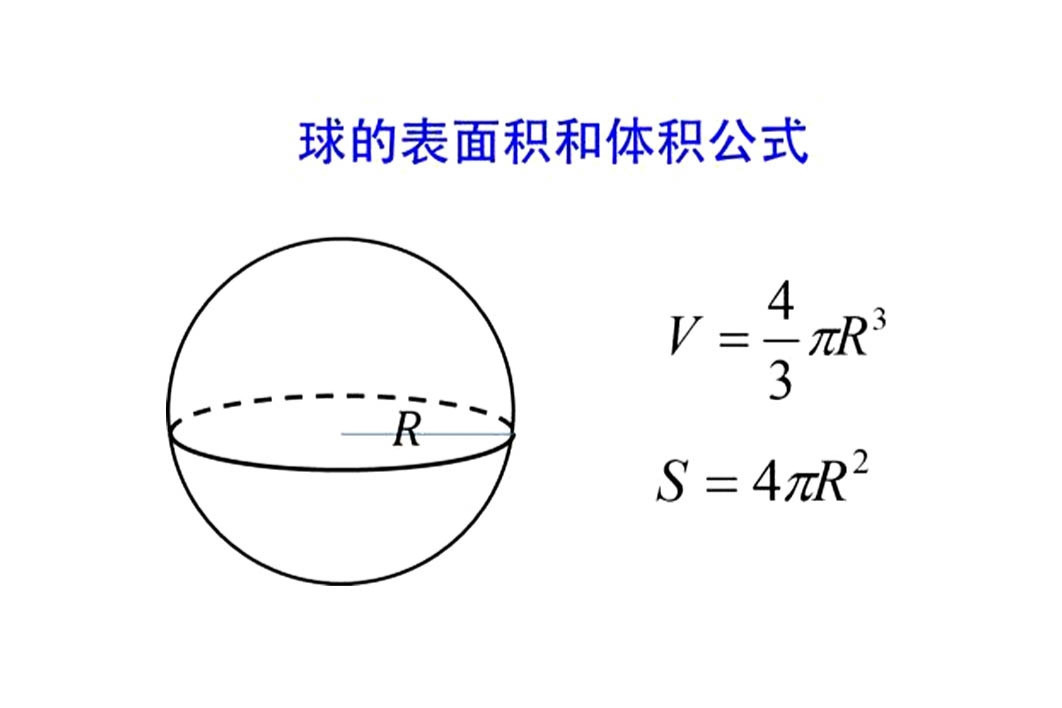



球体表面积 数学术语 搜狗百科




球の表面積と体積の公式 数学fun



高中数学 体积表面积公式 哔哩哔哩 Bilibili



培養孩子數學興趣 24 球的表面積爲什麼是4pr平方 人人焦點



計算球體面積的公式 球體面積是完整而準確的




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




球的體積公式球體表面積 球體表面積是指球面所圍成的幾何體的面積 它包括 Hktechno



体积计算公式大全图片 搜狗图片搜索



球的体积公式怎么求 球的体积和表面积的思维导图 碳资讯




球的表面积公式 趣智分享




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




012 球的体积空间几何体高中数学 Youtube




體表面積表初中數學 幾何 面積與體積公式 Uhlwc




體積公式球 Persemp



球的表面积和体积公式 搜狗图片搜索
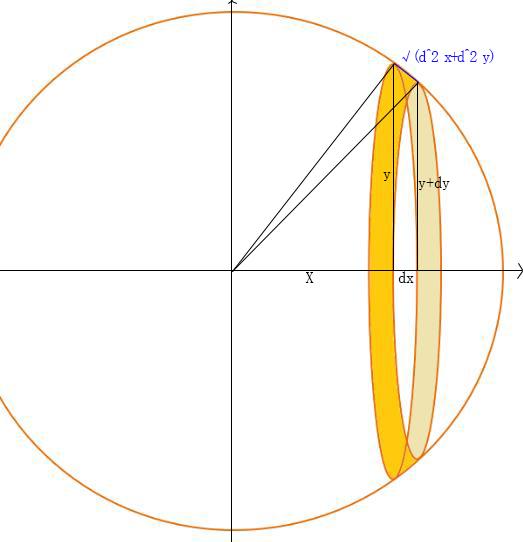



用积分推导球的表面积有哪些方法




圆锥与球与圆柱




球表面積公式377 Nbwsd




球の表面積と体積の公式 数学fun




14 平面及立體圖形 立體圖形的表面積及體積 齊齊溫




球的表面积公式是怎么推导出来的 Zhangjin11的博客 Csdn博客 球的表面积公式推导



球体体积公式推导图解 第1页 要无忧健康图库




圓柱體積公式 公式 釋義 圓周率 中文百科全書



1



球體表面積及體積的推導 每日頭條



球体表面积体积公式大全 球体体积计算公式22已更新 今日 更新 成人高考报名网 奥冠教育网
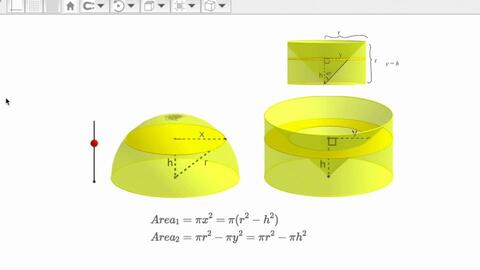



阿基米德是如何发现球体体积和表面积公式的 哔哩哔哩 Bilibili



球の体積と球の表面積の公式 求め方 証明や計算問題も解説 受験辞典




球體表面積算法球的表面積的求法 Prinejoy




Ppt 11 1 棱錐powerpoint Presentation Free Download Id



1
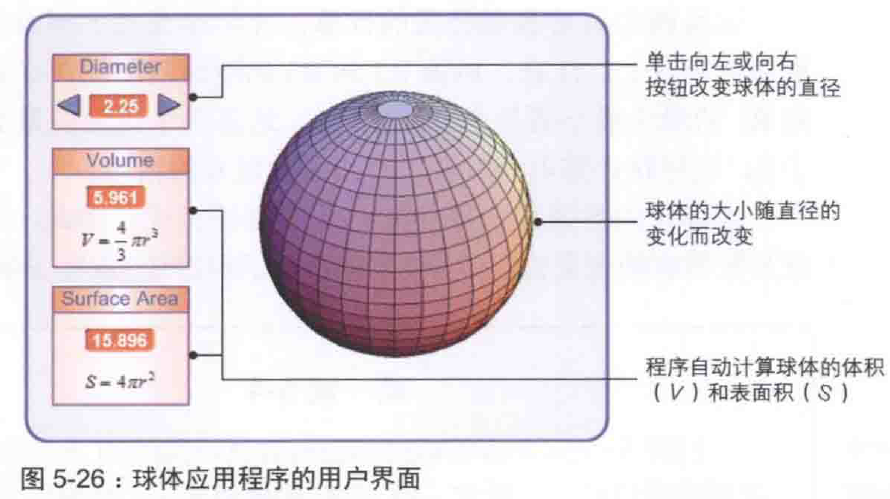



Scratch3 0计算球体体积和表面积 有间学堂 博客园




1 6 球的表面積與體積 Mathtsing高中數學 Youtube




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



球的體積求導便是球的表面積 互為逆運算 降維與升維 每日頭條




球體的體積與表面積 人人焦點



使用微积分推导出球体的体积公式v 4pr 3 3 哔哩哔哩 Bilibili




球體表面積 球體表面積是指球面所圍成的幾何體的面積 它包括球面和球面所圍 華人百科




球缺體積和球冠表面積的計算公式及應用 程式人生



球体表面积 快懂百科




球体的表面积和体积的计算公式 星火网校



球表面积公式和体积公式 高中数学系统教学文档必修二 洗地机之家
コメント
コメントを投稿